
Recently I downloaded a program called Y-Cruncher from a website (www.numberworld.org) and used it to generate 1 trillion digits of Pi. That's 1 million x 1 million - or 1,000,000,000,000 - digits. I thought it would be interesting to analyze the value to see what I could find.
But first, I had to modify my PC. I added 16 GB of RAM, increasing it from 32 GB to 48 GB. I also added 7 old disk drives we weren't using. Three of these were 6TB and four were 4TB, making an extra 34 terrabytes of disk storage. Y-Cruncher needs a lot of RAM and disk working space.
The disks wouldn't fit in the case, of course. They just had to lay around outside. My PC looked a bit odd for a while.
 |
It took Y-Cruncher 196 hours - 8.2 days - to generate 1,000,000,000,000 digits of Pi. Then I wrote several programs to analyze the output.
One thing I checked was the number of times each of the 10 digits - 0 through 9 - appeared. I was amazed to find that the counts were incredibly homogeneous. Out of 1,000,000,000,000 digits, each digit appeared very nearly 100,000,000,000 times, give or take about .00001%.
0 : 099,999,485,134 1 : 099,999,945,663 2 : 100,000,480,058 3 : 099,999,787,805 4 : 100,000,357,857 5 : 099,999,671,010 6 : 099,999,807,504 7 : 099,999,818,723 8 : 100,000,791,470 9 : 099,999,854,782 |
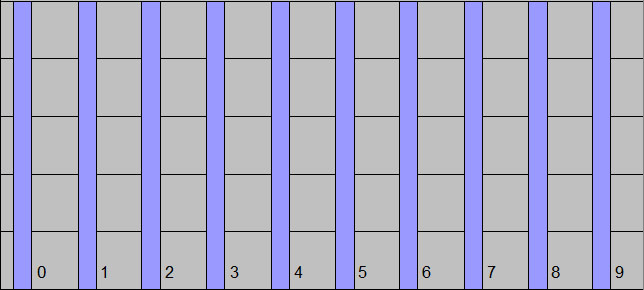 |
It's as though I was looking at the output of a very well written random number generator. I've written a few random number generators over the years. But I never took the time to generate a trillion digits and then analyze the output. However, I seriously doubt that I could have produced an output as homogeneous as this. And this wasn't produced by a RNG. It was produced by the Chudnovsky (1988) algorithm. According to Wiki, the formula looks like this:
 |
You can refer to Wiki if you want more information. I was a math major in college, but that was 50+ years ago, so my math is a bit rusty.
With such a statistically even distribution of the digits 0-9, it seems very likely that any given 9-digit number could be found 1,000 times within a field of 1,000,000,000,000 digits. Sure enough, I found Pat's 9-digit social security number 1,004 times and my SSN 957 times.
Similarly, any given 10-digit number might be found 100 times. And I found the following 10-digit sequences roughly 100 times each:
0123456789 |
94 times | |
9876543210 |
101 times | |
Our landline # w/area code |
75 times | |
Her cell # w/area code |
102 times | |
My cell # w/area code |
113 times |
A 12-digit sequence might be found only 1 time. And I found 777777777777 and 999999999999 one time each.
Interestingly, I found the 12-digit 141592653589 three times: positions 1-12, of course, but again starting in position 329,366,468,457 and also starting at 567,555,385,946.
Pi is a very interesting number. I'll keep examining it in my spare time.
Astronomy - Terrestrial Photos - Weather